Fishery-dependent length data
General guiding principles for the collection of length data
Length frequency data provide valuable information on population dynamics, including recruitment, growth, morphometric relationships, and mortality (Neumann and Allen 2007; Amoroso et al. 2024). Analyzing the length composition of a stock can offer insights into fishing mortality rate (Amoroso et al. 2024). The length composition of an unfished stock versus a fished stock can be noticeably different. For example, an unfished stock may display a high relative abundance of larger or older fish, while the length composition of an exploited population may show a lack of larger individuals and be dominated by smaller and younger fish (Amoroso et al. 2024). Additionally, length composition data may help identify inconsistent year-class strength and changes in growth (e.g., slow growth) (Anderson and Neumann 1996; Neumann and Allen 2007).
FishKit users commonly ask “Can I use my length dataset in FishKit?”. In short, the length dataset must meet scientific and statistical standards to be representative and to support intended application.
Correctly interpreting length composition data requires understanding how, when, and where data were collected (Neumann and Allen 2007; Amoroso et al. 2024). This information allows scientists to determine whether size structure changes across areas or over time, for instance, in response to management actions or differences in sampling gear (Neumann and Allen 2007). This information is crucial when analyzing length composition data, as it provides insight into the quantity and quality of the available data (Amoroso et al. 2024). Fisheries scientists must consider how the collected length composition may be influenced by sampling gear, the year and location of collection, and sample size (Neumann and Allen 2007; Amoroso et al. 2024). In simple terms, a non-selective fishing gear should reflect the true size distribution. However, selective fishing gear likely represents a sub-set of the size distribution of the fish population For one example, this may occur if a commercial fishery only targets and lands fish of a certain “plate size”. Correct characterization of the processes that gave rise to the observed length frequency is an important starting point for making inferences about fish stock health.
Several factors impact the representativeness of length composition data. For example, selectivity patterns (i.e., fishing gear) affect catch composition, often underrepresenting smaller fish relative to the fish population, which impacts the interpretation of length data. Market-based sampling sometimes combines catches from different areas and vessels, or both, but lacks contextual information about the fisheries, such as gear selectivity (Amoroso et al. 2024). Additionally, the size structure of fish may vary over time (seasonal changes in size structure) and space (area effects), affecting the representativeness and interpretation of composition data (Gulland and Rosenberg 1992; Neumann and Allen 2007; Amoroso et al. 2024). The proportion of landing sites or catch sampled, the sampling protocol, and the sex of the individuals sampled may bias the representativeness of the sampled composition data (Amoroso et al. 2024).
Length data collection programs should prioritize collecting samples with high precision over a geographical area that matches the extent of the stock. This means that sampling should be proportional to species density across different geographical areas, cover a temporal scale relevant to the intended analysis, and include all fishing gear types used to catch the fish (Amoroso et al. 2024). However, staff and budget constraints make optimal sampling challenging in real-world situations, particularly in data-limited fisheries. In such cases, when data are collected only in one area or are limited to one landing site or fishing gear, these limitations may lead to data that do not represent the population structure accurately and should be considered when analyzing and interpreting the data (Amoroso et al. 2024).
In some cases, length samples may not be representative of the size distribution of the population or stock, as they are not collected according to a rigorous statistical design (Gulland and Rosenberg 1992). Thus, developing an effective sampling design requires understanding the variability in length data, the types of analyses that will be applied to the data, and how errors impact precision and reliability. Such understanding can only be achieved after some initial data collection and evaluation of said data (Gulland and Rosenberg 1992). Therefore, an effective sampling design is an adaptive process that can be gradually improved over time.
Identifying an intended purpose of length sampling (e.g., evaluation of stock status, estimation of life history parameters) is also essential to implementing a sampling protocol. Doing so helps fisheries scientists better identify sampling design considerations and related challenges in gathering and analyzing this type of data. For instance, studies aimed at determining life-history parameters (e.g., growth or reproduction) often sample a wide range of lengths, including very small and very large fish. Such data are valuable for estimating biological parameters but may not accurately reflect the natural size distribution in the population or the catch nor be useful for purposes like stock assessment (Amoroso et al. 2024). Sample size needs also vary by objective. For example, estimating mean length or growth parameters generally requires a smaller sample size (Kritzer et al. 2001) compared to studies analyzing length frequencies (Miranda 2007). Additionally, species with different growth rates and asymptotic lengths (e.g., species that grow fast, like small pelagic, or slow-growth species) may require different sampling designs (Lai et al. 1996).
As an additional example of designing sampling in relation to intended purpose, consider the problem of tracking changes in a fish population over time using length composition. A standardized methodology may be crucial for avoiding bias introduced by the combination of gear, time, and area effects (Neumann and Allen 2007). Relying on a single gear type can help reduce bias because it allows for comparing size composition over time and across areas, ensuring the changes are not due to differences in selectivity. Similarly, the size structure of fish in samples may vary throughout the year (e.g., by season, month, or day), making it important to standardize sampling timing. Sampling locations should be chosen randomly or based on fixed criteria to avoid biases introduced by convenience (e.g., proximity), fish aggregations, or varying fish distribution patterns, such as habitat use or aggregation during spawning seasons (Neumann and Allen 2007).
- Fishery-dependent length data in the Data Repository
Gear selectivity effect
Different fishing gears may select individuals of different sizes. This selectivity is influenced by factors like gear mesh size, hook size, and the efficiency of the fishing gear, which may prevent, for example, the retention of smaller individuals (Neumann and Allen 2007). The selectivity of the fishing gear is a crucial factor influencing the length distribution of catches, as different fishing gears exhibit varying levels of selectivity, capturing certain sizes of fish more effectively than others (Gallucci et al. 1996). For instance, gill nets retain only a limited range of sizes based on mesh size, with fish of a particular size being more common in the catch and catch rates decreasing for both smaller and larger fish (i.e., dome-shaped selectivity) (Gallucci et al. 1996; Neumann and Allen 2007). Towed gears like seines allow smaller fish to escape easily, while larger fish are more frequently caught (Gallucci et al. 1996). Trap and hoop nets tend to select larger fish (Neumann and Allen 2007).
Therefore, fisheries scientists should take into account gear selectivity when analyzing length composition data collected by different fishing gears since the choice of gear directly impacts which length classes are most vulnerable to fishing mortality (Gallucci et al. 1996; Hubert 1996; Neumann and Allen 2007). Ignoring gear selectivity can lead to overestimating poorly selected length classes and underestimating highly selected ones (Gallucci et al. 1996).
Fish behavior also influences the effectiveness of certain fishing gear. For example, some gears (e.g., gill nets) are more likely to capture actively swimming fish, meaning more active or larger fish may be overrepresented in the catch. The location where the gear is set (e.g., depth, habitat type) also affects its effectiveness and influences fish encounters with the fishing gear (Neumann and Allen 2007). The latter can lead to size-selective gear avoidance, where larger fish may escape mobile gears but are more frequently encountered by fixed gears like longlines and gill nets.
When samples are obtained from market sampling, it can further complicate the issue of different selectivities. Market samples combine catches from different areas/vessels/gears and may not include harvested fish that are not commercially valuable, which can skew the length distribution. Additionally, fishers may keep smaller fish for personal consumption, leading to an underrepresentation of small fish in market samples (Amoroso et al. 2024).
Relevant Modules:
Size-related changes over time
Length composition samples can vary among seasons, even when standardized fishing gear is used, as fish physiology and behavior change throughout the year (Pope and Willis 1996; Neumann and Allen 2007). For example, Carline et al. (1984) found that larger largemouth bass tend to move offshore after spawning, making them less vulnerable to capture in the summer, and then return to inshore areas as the water cools in the fall. Pope and Willis (1996) also described seasonal changes in size structure for several freshwater species, and spring and fall peaks in size structure have been observed in various species, such as bluegill (Bettross and Willis 1988), yellow perch (Lott and Willis 1991), and walleye and sauger (Mero and Willis 1992).
Fish may also change their depth distribution over time in response to changes in temperature and food availability. These changes can influence the sizes of fish captured by gear types that operate at specific depths (Pope and Willis 1996). Additionally, many species form aggregations during certain times of the year (e.g., spawning aggregations), making them more vulnerable to fishing and resulting in a higher proportion of larger, mature individuals being caught. If sampling efforts are not well distributed across the year, mature large fish may overrepresent the size distribution during spawning periods (Amoroso et al. 2024). A similar situation can occur with species that present strong recruitment pulses, since a large proportion of small fish may skew the length distribution toward small individuals (Amoroso et al. 2024).
Relevant Modules:
Size-related changes in space (area effect)
Length composition data may vary depending on the sampling area, with varying sizes and densities of fish across areas. For instance, some species undergo ontogenetic habitat shifts, exhibit migratory behaviors, and occupy different juvenile and adult habitats (Gulland and Rosenberg 1992). Size-based territoriality and aggregation behaviors (e.g., offshore/inshore movements during spawning or specific habitat use) can also influence spatial size distribution (Pope and Willis 1996), thereby affecting fish vulnerability relative to the placement of fishing gear. Variations in fish lengths by area can also result from factors like different gear types, spatial gradients in size distribution, varying growth rates across regions, and market preferences for particular sizes (Amoroso et al. 2024). Consequently, it is thus unlikely that any sampling design will be able to take a representative sample of the entire fish population or stock. However, samples should be collected widely in space and time, as broader spatial coverage can yield a more representative picture of the population size structure (Gulland and Rosenberg 1992).
Length composition data should be ideally representative of all areas. When data from catch or landings encompass multiple geographic locations, evaluating the number of samples per area and year is essential to assess potential bias (Amoroso et al. 2024). Ideally, monthly samples should be taken across all areas and fleets, as unbalanced sampling may create differences in length composition data between years and areas unrelated to fishing mortality or changes in size structure (Amoroso et al. 2024).
Some studies emphasize the importance of sampling a wide range of locations to enhance length data representativeness. For example, Pennington et al. (2002) noted that sampling more locations yields better spatial representation than simply increasing fish counts at fewer sites, and Miranda (2007) emphasized that the accuracy of length sampling is subject to choosing appropriate sampling gear and locations. Thus, broad spatial coverage across diverse areas is crucial for obtaining representative length data in fisheries. Understanding data coverage helps anticipate interpretation issues and informs how best to utilize collected data (Amoroso et al. 2024).
Relevant Modules:
Statistical properties of sampling
A well-designed statistical sampling method aims to collect a representative sample with low variance (high precision) and minimal bias (Gulland 1966; Conquest et al. 1996). Bias and variance are largely independent; for instance, a sample may exhibit low variance (consistent estimates) but still have high bias (estimates far from true values) (Gulland 1966). Improving precision does not necessarily reduce bias. Both bias and precision must be addressed to obtain accurate and reliable length composition data representing the entire stock.
Bias is the difference between the average of estimated values and the true value. It reflects systematic error, often caused by poor sample selection or collection methods rather than analysis errors (Gulland 1966; Stamatopoulos 2002). For example, size estimates can be biased if samples disproportionately include larger fish. Variance, on the other hand, refers to the spread of estimates around their average; lower variance indicates greater precision (Gulland 1966). While increasing the sample size reduces variance, it does not address bias, which can typically only be managed by refining the sampling process (Gulland 1966).
Standard statistical texts recommend using a stratified, multi-stage sampling design for length sampling (Cochran 1953; Gulland 1966), along with the following general guidelines:
- Distribute sampling across different landing locations to avoid concentrating efforts in the most convenient areas.
- Measure fish from multiple vessels to reduce intra-haul correlation and increase representativeness.
- Apply proportional sampling, where the amount of sampling in each stratum (area, vessel, or landing site) corresponds to its contribution to overall variability (e.g., more sampling in strata with larger landings or greater size variability).
- Determine sample sizes at each stage (e.g., number of fish per vessel or number of vessels per site) based on the costs of increasing the number of samples (sampling more vessels or sites) versus taking larger samples within each vessel or site. The goal is to balance sampling costs with the need for accurate data, prioritizing information quality over quantity (e.g., two samples of 150 fish from different sources are likely more informative than one sample of 300 fish from the same source) (Gulland and Rosenberg 1992).
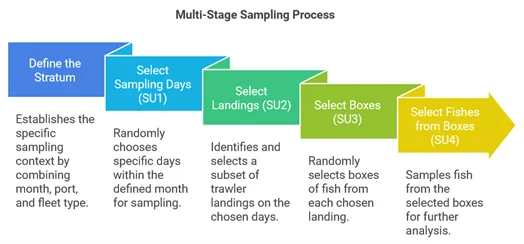
The following steps outline a multi-stage sampling design for length composition data from annual landings based on (Cadima 2005). First, fishery scientists should define the stock of interest. The stock of interest represents the target species harvested by the entire fleet and landed at all ports within the study area over a specified period (e.g., one year).
Second, the total landings, representing the population or stock to be sampled, are divided into strata based on separation by month, fleet component (e.g., trawlers, purse seiners), and landing port (e.g., Port A, B, or C). The number of strata is the product of these three components. For example, 12 months × 2 fleet components × 3 ports result in 72 strata. This initial population stratification accounts for potential differences in annual length distribution caused by seasonality, fishing gear, and location (i.e., time, gear, and area effects). All strata must be sampled, and multiple sampling events (e.g., trips, vessels, etc.) are necessary from each stratum.
Third, a multi-stage sampling approach should be carried out and applied to each stratum. For example, one stratum is defined by a fleet category, a landing port, and a specific month (e.g., landing in Port A during January). The multi-stage sampling begins by randomly selecting several days within the month for sampling in stratum 1. Each selected day corresponds to the first sampling unit (SU1). Next, several trawler landings are randomly chosen for each selected day, with each landing representing the second sampling unit (SU2). Following this, several boxes of fish are randomly selected from each chosen trawler landing, with each box representing the third sampling unit (SU3). Finally, from each selected box, fish are randomly selected (without replacement—meaning the fish is not returned to the box and cannot be selected again in the same sampling procedure) and measured for their length. The individual fish constitute the fourth sampling unit (SU4).
In the final stage, the fish stock’s length composition (size distribution) is calculated based on the fourth sampling unit. This data is then scaled up (raised) through successive back calculations to represent the entire stratum, ensuring it reflects all trawler landings in Port A during January. This multi-stage procedure (Figure X) is repeated for all strata (e.g., 72 strata in this example). A detailed description with examples can be found in Cadima (2005).
After measuring the number of fish (buckets) from each selected box, data needs to be organized into length classes, and the frequencies for each class need to be calculated. Next, the data is scaled up (raised) to the box level, landing, day, and stratum level using appropriate conversion factors. This process should be repeated for all strata. Each step progressively scales up the sample data to represent the entire stratum and, ultimately, the entire stock, ensuring that the length composition is accurately represented across the fishery (for a detailed example, see (Cadima 2005).
Relevant Modules:
Techniques to reduce bias and improve precision of length sampling
One of the most important techniques for reducing bias and improving precision is selecting samples using a well-defined design to ensure the sample represents the length structure of the population and can be used to make inferences about the population (Gulland 1966; Gulland and Rosenberg 1992). Random sampling is the most direct way to achieve a representative sample (Gulland and Rosenberg 1992), often combined with a stratified, multi-stage sampling design (Cadima 2005). However, achieving a truly random sample can be challenging when sampling from catches. It is essential to recognize that haphazard sampling is not a substitute for random sampling. Without a structured approach, unconscious patterns may emerge and bias the results (Cadima 2005).
Bias arises from systematic errors that result in unrepresentative samples of the true fish length distribution. A significant source of bias is gear selectivity, where different fishing gears capture fish sizes with varying probabilities (Amoroso et al. 2024). For instance, using selective gear to collect length samples can produce a biased length composition (e.g., underestimating smaller fish). Another source of bias is market sampling, which can occur when fishers retain specific sizes for personal use or when the market demands specific sizes, leading to the underrepresentation of smaller fish (Amoroso et al. 2024). To minimize these biases, collecting samples from all fleets is critical. When onboard sampling is not feasible, sampling should occur immediately after landing, before market sorting. If sampling occurs after market selection, it is essential to sample from all market categories and appropriately weigh the samples to reflect their contribution to total landings (Amoroso et al. 2024).
Another important consideration is avoiding the concentration of sampling on a few vessels or a few specific fishers, with a large number of fish measured from each. Fish landed by one vessel at one time are likely to be of similar size; thus, sampling two boxes of fish from the same vessel may provide the same information as sampling one box due to intra-haul correlation (Pennington et al. 2002). A similar situation may arise when repeatedly sampling a vessel that lands at a conveniently located port or sampling at a nearby market consistently supplied by the same few vessels. This approach may result in bias if these catches are not representative of the spatial distribution and fishing gear used by the entire fleet. A more optimal sampling strategy would likely include collecting samples from more vessels, stations, or locations rather than simply increasing the number of fish measured in each station/vessel/location (Pennington et al. 2002).
Precision in length composition sampling refers to the reproducibility or consistency of measurements (Gulland and Rosenberg 1992). Larger sample sizes typically help improve precision (Gulland and Rosenberg 1992; Cadima 2005). Precision can also be improved by applying appropriate sampling designs that ensure representative data collection, such as stratified random, cluster, or multi-stage designs (Cadima 2005). These methods minimize sampling variance and improve the precision of length composition estimates. Consistent and well-defined observation techniques are also essential for improving precision. For example, all samplers must use the same method for measuring length (e.g., fork length or total length) and record data with consistent precision (e.g., to the nearest unit or below the unit) (Gulland and Rosenberg 1992).
Optimizing sample size and allocation is also important for improving precision. While larger sample sizes result in greater precision, optimal allocation across strata is necessary to maximize precision within budget or time constraints. Pennington et al. (2002) found that an effective way to improve precision is increasing the number of strata (e.g., stations, locations, vessels) instead of just increasing the number of fish sampled in each station. Analyzing and understanding the sampling distribution through estimates of sampling variance and standard errors as sampling progresses over time is essential for making reliable conclusions about the data and adjusting the sampling process.
When samples have already been collected, analysts are often interested in assessing the precision of the data before using it. One approach to analyzing the information contained in the data is to estimate the realized or effective sample size. An important consideration is that length samples from fishery-dependent (or fishery-independent) sampling may not represent a random sample of the entire population. Therefore, the realized sample size (or effective sample size) is not simply the number of fish measured but rather the number of independent samples obtained (Stewart and Hamel 2014). The effective sample size can be defined as the sample size that would need to be collected randomly to provide the equivalent amount of information contained in the observed sample (Pennington et al. 2002). Thus, although M total length observations may have been collected, the effective sample size is typically smaller than the actual number of individuals measured. This effective sample size is strongly influenced by intra-haul correlation, also known as cluster sampling correlation (e.g., within-trip correlation) (Chih 2011), because individuals within a cluster tend to be more similar to each other than to individuals in the overall population. This reduces the amount of information contained in the sample. Stewart and Hamel (2014) emphasize that intra-haul correlation is a more significant determinant of the effective sample size than the actual number of fish measured. Chih (2011) demonstrated that cluster sampling of length data reduces the precision of both mean length and total mortality estimates. They found that the effective sample size was significantly lower than the actual sample size, approximately 2.9% of the total fish sampled. Therefore, scientists should prioritize increasing the number of sampling units rather than merely maximizing the number of fish measured within each haul or cluster.
Relevant Modules:
Some sample size considerations and adaptive sampling
This process defines an ideal sampling protocol, but adaptations are often needed to meet the capacity-limited realities of small-scale, data-limited fisheries. FishKit users may use the same phases, and adjust this protocol by…..
Conducting adequate length composition sampling to produce unbiased estimates with minimal variance is particularly challenging in data-limited situations and requires careful planning (Gulland and Rosenberg 1992). One critical factor is that fish landed by the same vessel (or at the same port) tend to have similar sizes compared to samples from multiple vessels or ports. This phenomenon, known as intra-haul correlation, means fish caught together tend to have similar lengths (Pennington et al. 2002; Harford and Rios 2018).
Intra-haul correlation affects the effective sample size, which reflects the amount of information a sample provides about a population. The effective sample size represents the number of fish that should have been randomly sampled to achieve the same precision as a clustered sample (the current sample) (Pennington et al. 2002; Harford and Rios 2018). This clustering effect typically reduces the effective sample size because fish caught together often share similar traits, diminishing the statistical power of the sampling (Pennington et al. 2002). As a result, measuring additional boxes from the same vessel may add little information about the overall size structure of the population. Even if fewer fish are measured per vessel, sampling from more vessels is more informative than increasing the sample size from any single vessel (Gulland and Rosenberg 1992).
When determining the optimal sampling design and intensity for collecting length composition data, scientists often encounter the challenge that robust sampling design and optimal sample size cannot be achieved immediately. First, it is necessary to gain some understanding of the variability in length composition data (Gulland and Rosenberg 1992). The question of how many fish to measure is complex, with the answer depending on the existing sampling design, the biological characteristics of the fish stock, and the intended use of the length data set (e.g., estimation of growth parameters, length frequency, or mean length) (Gulland and Rosenberg 1992; Kritzer et al. 2001). Conducting pilot studies to characterize basic population features can help inform the required sample size for achieving desired precision levels (Kritzer et al. 2001).
In the early stages of sampling, the focus should be on achieving broad coverage across seasons, locations, and gear types, ideally through many smaller samples rather than a few large ones. Also, a random and stratified, multi-stage sampling design can improve data quality and representativeness in the early stages of sampling. However, it is important to understand that the variability in the data will only become apparent over time. This gradual understanding allows researchers to refine the sampling design, adjust sample sizes, and address bias and sampling errors (i.e., adaptive sampling) (Gulland and Rosenberg 1992).
The choice of an optimal sample size for length composition data is influenced by variance between and within units (e.g., vessels, areas) (Gulland 1966). Several studies have evaluated the impact of sample size on demographic parameter estimates. For instance, Kritzer et al. (2001) used a bootstrapping approach to investigate the effect of sample size on the precision of population parameters. Bootstrapping approaches are valuable as they simulate repeated sampling from a population without needing additional data collection, which is particularly useful in data-limited situations, although initial data is required to implement this approach. (Kritzer et al. 2001) found that parameters such as mean length in the catch can be estimated with small sample sizes, similar to findings by Wang et al. (2020). However, more complex model parameters, such as von Bertalanffy growth parameters, require larger sample sizes to achieve high precision.
When the goal is to build a reliable length frequency to understand the population’s size structure, sample size requirements may differ. The required sample size for describing length composition is often related to life history processes such as growth, mortality, and movement, and it varies by species (Wang et al. 2020). Additionally, the sample size for length frequency analysis depends on the length interval size used. Smaller length intervals provide finer detail but require larger samples for accurate representation. In contrast, larger intervals (e.g., 10 cm for large species like tuna) are more likely to reflect the true length distribution with limited sample sizes (Wang et al. 2020).
It is crucial to have clarity about the purpose of data collection and to consider the trade-off between desired precision and the cost of additional sampling (Kritzer et al. 2001). While larger sample sizes generally yield more reliable results, this improvement follows the law of diminishing returns, where additional samples yield only marginal gains in precision beyond a certain point (Kritzer et al. 2001). Regular reviews of sampling programs are vital for improving data quality over time (i.e., adaptive sampling) (Kritzer et al. 2001). Ultimately, sampling design and sample size should be refined (i.e. adaptive sampling) based on the statistical properties (e.g., variance) of the collected data (Gulland and Rosenberg 1992; Kritzer et al. 2001).
Relevant Modules: